Optimization & Regularization

In this notebook, we will focus on the optimization and regularization aspects of deep learning.

Optimizers are algorithms that iteratively adjust the parameters of a neural network to minimize the loss function during training. They define how the networks learn from the data.

Let’s denote $\hat{\mathcal{R}}(\theta)$ as the empirical risk function, which assigns the empirical risk given data $\{(x^{(i)}, y^{(i)})\}_{i = 1}^n$ to a parameter vector $\theta$. Here, $f_\theta$ is the model’s prediction function, $x^{(i)}$ is the $i$-th sample in the training data, and $y^{(i)}$ is the corresponding target value. \[\hat{\mathcal{R}}(\theta) = \frac{1}{n} \sum_{i=1}^n L(f_\theta(x^{(i)}), y^{(i)}) \]

Often, the empirical risk function is extended with a regularization term. Regularization in machine learning and statistics is used to prevent overfitting by adding a penalty term to the risk function, which discourages overly complex models that might fit noise in the training data. It helps improve generalization to unseen data. One common regularizer is the L2 norm of the parameter vector, which penalizes large coefficients by adding the squared magnitude of the coefficients to the loss function:

\[ \hat{\mathcal{R}}_{\text{reg}}(\theta) = \hat{\mathcal{R}}(\theta) + \lambda \sum_{j=1}^p \theta_j^2 \]

Here, $\lambda$ controls the strength of the regularization, i.e., the trade-off between fitting the training data and keeping the parameters small. This encourages the model to prefer less complex solutions, where complexity is measured by the L2 norm of the coefficients. As a result, parameter vectors will have entries closer to the zero vector, a concept known as parameter shrinkage.

Quiz: Regularization

Question 1: Different Scales: Is it a problem for L2-regularization when the features have different scales? What can we do about it?

Click for answer

Yes, because the size of the parameter vector depends on the scale of the features. Consider the marginal effect of an additional cent on GDP vs. the effect of an additional euro. To avoid this, we can normalize the features so they all have the same scale.

While the goal of the risk function is to define what we want, it’s the optimizer’s job to find the parameter vector $\theta^*$ that minimizes the empirical risk function. For simplicity, we will now refer to both the regularized and unregularized risk function as $\hat{\mathcal{R}}$.

\[\theta^* = \arg \min_\theta \hat{\mathcal{R}}(\theta)\]

This is done by iteratively updating the parameter vector $\theta$ using the gradient of the loss function with respect to the parameter vector. The simplified update formula for a parameter $\theta$ at time step $t$ is given by:

\[\theta_{t+1} = \theta_t - \eta \frac{\partial \hat{\mathcal{R}}}{\partial \theta_t}\]

Where:

$\theta_t$ is the current value of the parameter vector at time step $t$.
$\theta_{t+1}$ is the new value of the parameter after the update.
$\eta$ (eta) is the learning rate, which controls the step size.
$\frac{\partial \hat{\mathcal{R}}}{\partial \theta_t}$ is the derivative of the empirical risk function $\hat{\mathcal{R}}$ with respect to parameter $\theta$, i.e., the gradient.

Quiz: Learning Rate

Question 1: Can you explain what happens when the learning rate is too high? What happens when it is too low?

Click for answer

A too high learning rate will cause the parameters to overshoot the minimum and diverge. A too low learning rate will cause the parameters to converge slowly.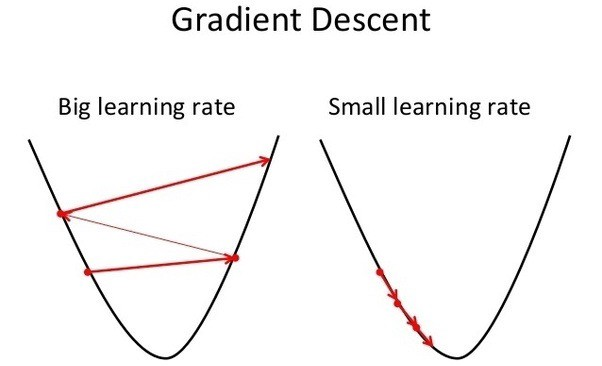

Source

The optimizers used in practice differ from the above formula, as:

The gradient is estimated from a batch rather than the entire training dataset.
The simplistic update formula is extended with:
- Weight decay
- Momentum
- Adaptive learning rates

Before we cover these more advanced approaches (specifically their implementation in AdamW), we will first focus on the vanilla version of Stochastic Gradient Descent (SGD).

Mini-Batch Effects in SGD

When using mini-batches, the gradient becomes a noisy estimate of the gradient over the full dataset. With $\nabla L^{(i)}_t := \frac{\partial L^{(i)}}{\partial \theta_t}$ being the gradient of the loss function with respect to the entire parameter vector estimated using $(x^{(i)}, y^{(i)})$, the mini-batch gradient is given by:

\[\nabla L^B_t = \frac{1}{|B|} \sum_{i \in B} \nabla L^{(i)}_t\]

where $B$ is the batch of samples and $|B|$ is the batch size.

The update formula for SGD is then given by:

\[\theta_{t+1} = \theta_t - \eta \nabla L^B_t\]

This is visualized in the image below:

Quiz: Vanilla SGD

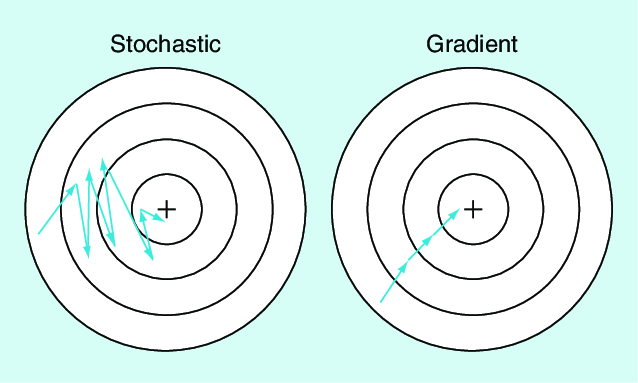
Question 1: What happens when the batch size is too small or too large?

Click for answer

Trade-offs with Batch Size:

Larger batches provide more accurate gradient estimates.
Smaller batches introduce more noise but allow more frequent parameter updates.

Question 2: The mini-batch gradient is an approximation of the gradient over the full dataset. Does the latter also approximate something? If so, what?

Click for answer

In machine learning, we assume that the data is drawn from a distribution $P$. The gradient over the full dataset approximates the expectation over this distribution:

\[\nabla \mathcal{R} = \mathbb{E}_{x \sim P} \nabla \mathcal{L}(f_\theta(x), y)\]

Because deep learning models can have many parameters and computing gradients is expensive, understanding the effects of different batch sizes and convergence is important. The computational cost (which we define as the time it takes to perform one optimization step) of a gradient update using a batch size $b$ consists of:

Loading the batch into memory (if the data does not fit into RAM).
The forward pass of the model.
The backward pass of the model.
The update of the parameters.

We will discuss point 1 later, and point 4 does not depend on the batch size, so we can ignore it.

Quiz: Bang for Your Buck

Question 1: True or false: The cost (duration) of performing a gradient update using a batch size of $2$ is twice the cost of a batch size of $1$.

Click for answer

False. Because GPUs can perform many operations simultaneously, the cost of performing a gradient update using a batch size of $2$ is not twice the cost of a batch size of $1$. The cost depends on many factors, but if the model is small, the cost of a batch with 2 observations might be almost the same as one with one observation.

Question 2: The standard error of the mini-batch gradient estimate (which characterizes the precision of the gradient estimate) can be written as:

\[\text{SE}_{\nabla L^B_t} = \frac{\sigma_{\nabla L_t}}{\sqrt{|B|}}\]

where $\sigma_{\nabla L_t}$ is the standard deviation of the gradient estimate relative to the batch size.

Describe the dynamics of the standard error when increasing the batch size: How do you need to increase a batch size from $1$ to achieve half the standard error? What about increasing a batch size from $100$?

Click for answer

The standard error decreases as the batch size increases, but with diminishing returns. To halve the standard error:

Increase the batch size from $1$ to $4$.
Increase the batch size from $100$ to $400$.

This is because the standard error is inversely proportional to the square root of the batch size.

Mini-Batch Gradient Descent: It’s not all about runtime

As we have now covered some of the dynamics of a simple gradient-based optimizer, we can examine the final parameter vector $\theta^*$ that the optimizer converges to. When using a gradient-based optimizer, the updates will stop once the gradient is close to zero. We will now discuss the type of solutions where this is true and their properties.

We need to distinguish saddle points from local minima from global minima:

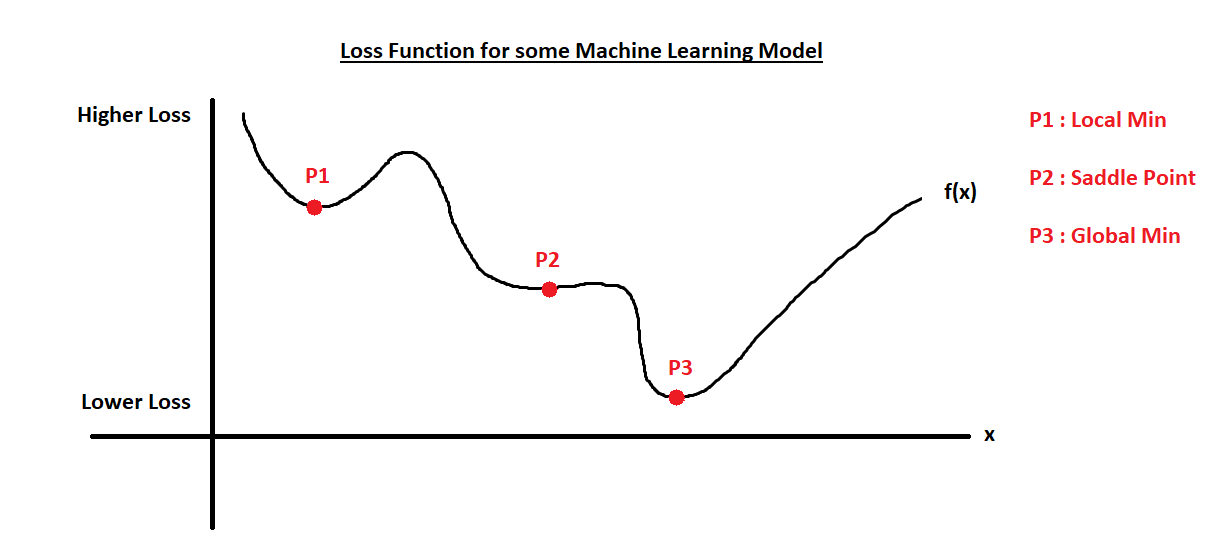
In deep learning, where high-dimensional parameter spaces are common, saddle points are more likely to occur than local minima. However, due to the stochastic nature of SGD, optimizers will find local minima instead of saddle points.

Quiz: Local vs. Global Minima, Generalization

Question 1: Do you believe SGD will find local or global minima? Explain your reasoning.

Click for answer

Because the gradient only has local information about the loss function, SGD finds local minima.

Question 2: Assuming we have found a $\theta^*$ that has low training loss, does this ensure that we have found a good model?

Click for answer

No, because we only know that the model has low training loss, but not necessarily low test loss.

SGD has been empirically shown to find solutions that generalize well to unseen data. This phenomenon is attributed to the implicit regularization effects of SGD, where the noise introduced by mini-batch sampling helps guide the optimizer towards broader minima with smaller L2 norms. These broader minima are typically associated with better generalization performance compared to sharp minima.

Source

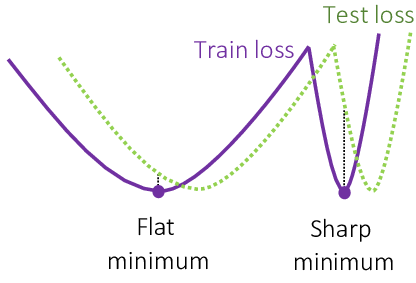
These properties are also known as implicit regularization of SGD. Regularization generally refers to techniques that prevent overfitting and improve generalization. There are also explicit regularization techniques, which we will cover next.

Weight Decay

One modification to the SGD update formula is the so-called weight decay, which is equivalent to adding a regularization penalty term to the loss function as we have seen earlier.

Note

For more complex optimizers such as Adam, weight decay is not equivalent to adding a regularization penalty term to the loss function (Loshchilov 2017). However, the main idea of both approaches is still to shrink the weights to $0$ during training.

If we integrate weight decay into the gradient update formula, we get the following:

\[\theta_{t+1} = \theta_t - \eta \big(\frac{\partial L}{\partial \theta_t} - \lambda \theta_t\big)\]

This formula shows that the weight decay term ($- \lambda \theta_t$) effectively shrinks the weights during each update, helping to prevent overfitting.

Source

Momentum

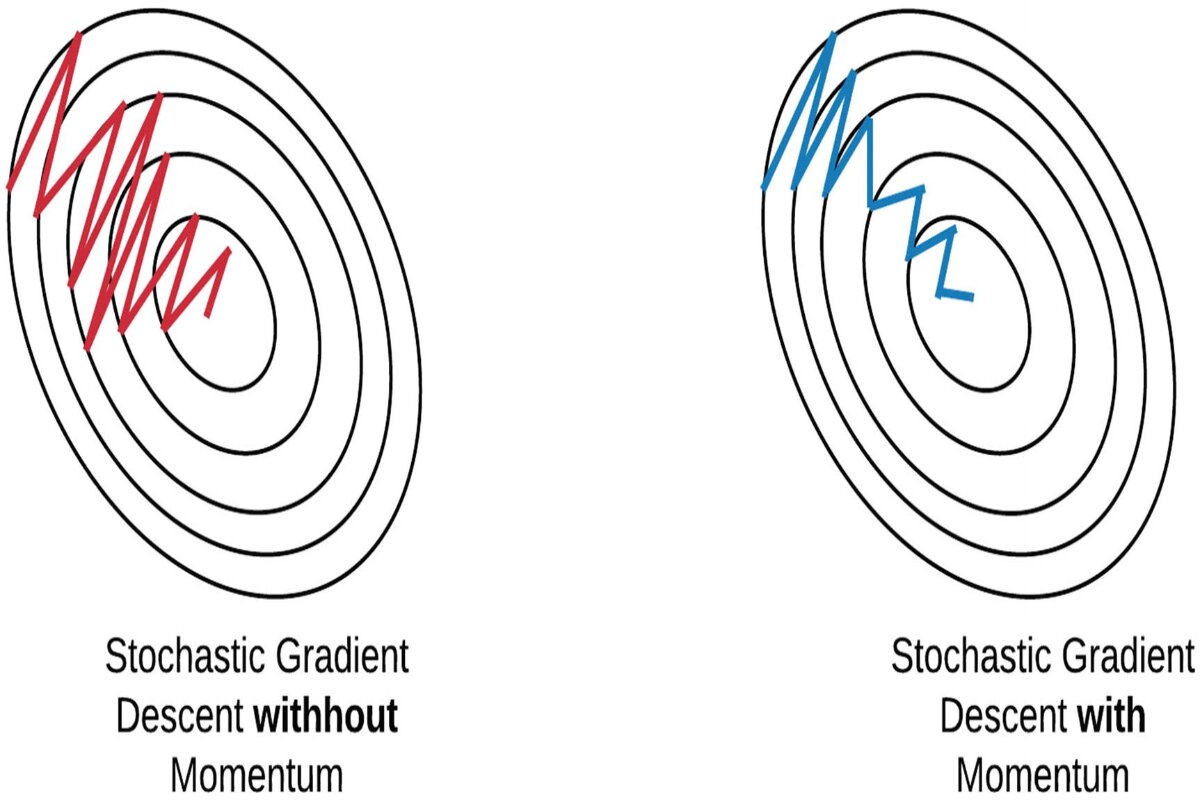
Momentum is a technique that helps accelerate gradient descent by using an exponential moving average of past gradients. Like a ball rolling down a hill, momentum helps the optimizer:

Move faster through areas of consistent gradient direction.
Push through sharp local minima and saddle points.
Dampen oscillations in areas where the gradient frequently changes direction.

The exponential moving momentum update can be expressed mathematically as:

\[ (1 - \beta) \sum_{\tau=1}^{t} \beta^{t-\tau} \nabla_{\theta} \mathcal{L}(\theta_{\tau-1}) \]

In order to avoid having to keep track of all the gradients, we can calculate the update in two steps as follows:

\[ v_t = \beta_1 v_{t-1} + (1 - \beta_1) \nabla_\theta L(\theta_t) \]

\[ \theta_{t+1} = \theta_t - \eta \frac{v_t}{1 - \beta_1^t} \]

The hyperparameter $\beta_1$ is the momentum decay rate (typically 0.9), $v_t$ is the exponential moving average of gradients, and $\eta$ is the learning rate as before. Note that dividing by $1 - \beta_1^t$ counteracts a bias because $v_0$ is initialized to $0$.

Source

Adaptive Learning Rates

Adaptive learning rate methods automatically adjust the learning rate for each parameter during training. This is particularly useful because:

Different parameters may require different learning rates.
The optimal learning rate often changes during training.

Before, we had one global learning rate $\eta$ for all parameters. However, learning rates are now allowed to:

Change over time.
Be different for different parameters.

Our vanilla SGD update formula is now generalized to handle adaptive learning rates:

\[\theta_{t+1} = \theta_t - \eta_t \cdot \frac{\nabla_\theta L(\theta_t)}{\sqrt{v_t} + \epsilon}\]

Here, $\eta_t$ is now not a scalar learning rate, but a vector of learning rates for each parameter, and ‘$\cdot$’ denotes the element-wise multiplication. Further, $\epsilon$ is a small constant for numerical stability.

In AdamW, the adaptive learning rate is controlled by the second moment estimate (squared gradients):

\[v_t = \beta_2 v_{t-1} + (1-\beta_2)(g_t)^2\] \[\hat{\eta}_t = \eta \frac{1}{\sqrt{v_t + \epsilon}}\]

In words, this means: In steep directions where the gradient is large, the learning rate is small and vice versa. The parameters $\beta_2$ and $\epsilon$ are hyperparameters that control the decay rate and numerical stability of the second moment estimate.

When combining weight decay, adaptive learning rates, and momentum, we get the AdamW optimizer. It therefore has parameters:

lr: The learning rate.
weight_decay: The weight decay parameter.
betas: The momentum parameters ($\beta_1$ and $\beta_2$).
eps: The numerical stability parameter.

Note that AdamW also has another configuration parameter amsgrad, which is disabled by default in torch, but which can help with convergence.

Optimizers in torch

torch provides several common optimizers, including SGD, Adam, AdamW, RMSprop, and Adagrad. The main optimizer API consists of:

Initializing the optimizer, which requires passing the parameters of the module to be optimized and setting the optimizer’s hyperparameters such as the learning rate.
step(): Update parameters using current gradients.
zero_grad(): Reset gradients of all the parameters to zero before each backward pass.
Just like nn_modules, they have a $state_dict() which can, for example, be saved to later load it using $load_state_dict().

We will focus on the AdamW optimizer, but the others work analogously.

library(torch)
formals(optim_adamw)

$params


$lr
[1] 0.001

$betas
c(0.9, 0.999)

$eps
[1] 1e-08

$weight_decay
[1] 0.01

$amsgrad
[1] FALSE

To construct it, we first need to create a model and then pass the parameters of the model to the optimizer so it knows which parameters to optimize.

model = nn_linear(1, 1)
opt <- optim_adamw(model$parameters, lr = 0.2)

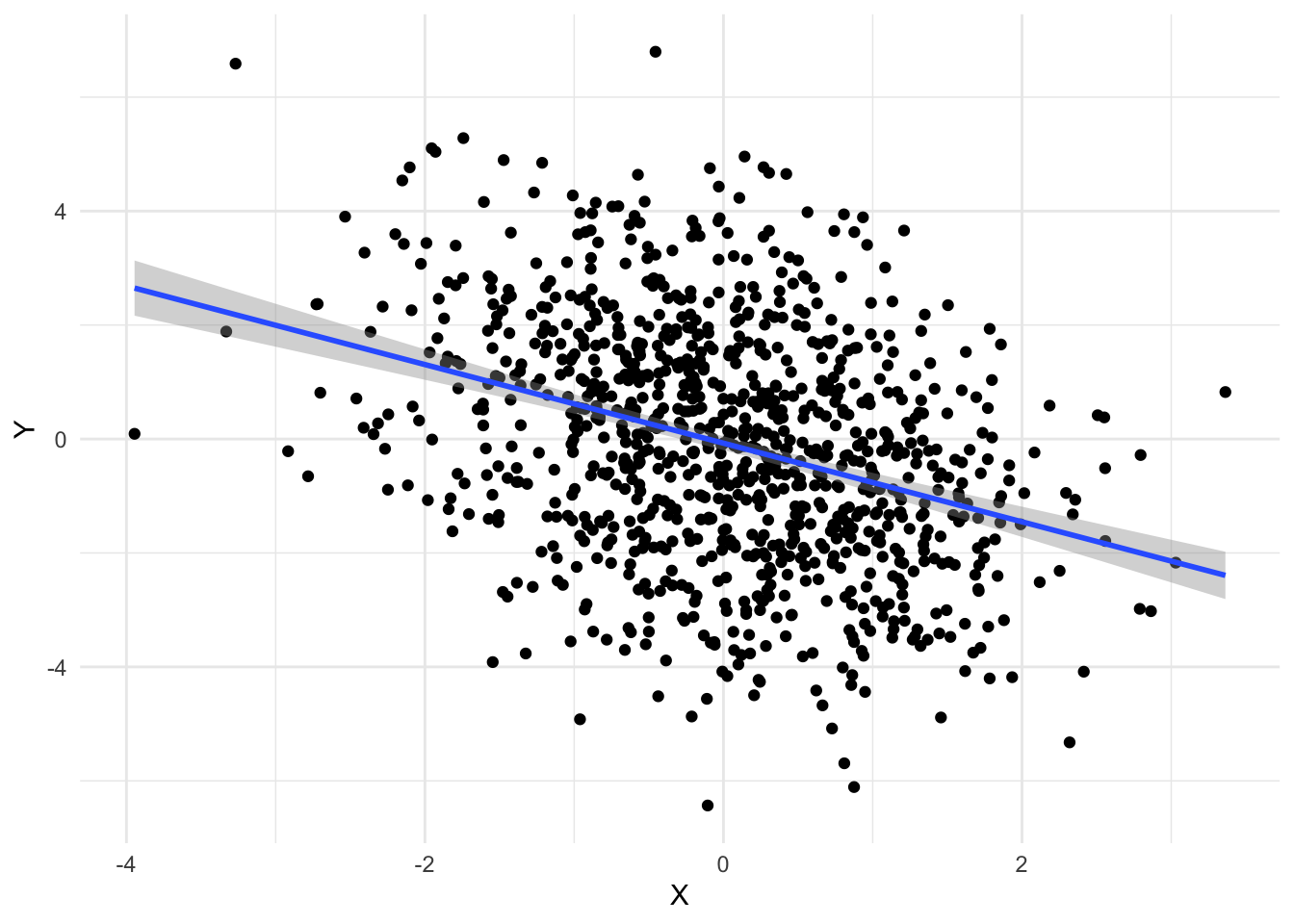
To illustrate the optimizer, we will again generate some synthetic training data:

torch_manual_seed(1)
X <- torch_randn(1000, 1)
beta <- torch_randn(1, 1)
Y <- X * beta + torch_randn(1000, 1) * 2

This represents data from a simple linear model with some noise:

Performing a (full) gradient update using the AdamW optimizer consists of:

Calculating the forward pass
```
y_hat = model(X)
```
Calculating the loss
```
loss = mean((y_hat - Y)^2)
```
Performing a backward pass
```
loss$backward()
```
Applying the update rule
```
opt$step()
```

Note that after the optimizer step, the gradients are not reset to zero but are unchanged.

model$weight$grad

torch_tensor
 0.5993
[ CPUFloatType{1,1} ]

If we were to perform another backward pass, the gradient would be added to the current gradient. If this is not desired, we can set an individual gradient of a tensor to zero:

model$weight$grad$zero_()

torch_tensor
 0
[ CPUFloatType{1,1} ]

Optimizers also offer a convenient way to set all gradients of the parameters managed by them to zero using $zero_grad():

opt$zero_grad()

Quiz: Guess which parameter is varied

We will now show some real trajectories of the AdamW optimizer applied to the linear regression problem from above where one specific parameter is varied. Recall that:

$\eta$: The learning rate controls the step size of the optimizer.
$\lambda$: The weight decay parameter controls the bias of the optimization towards a parameter being close to zero. A value of $0$ means no weight decay.
$\beta_1$: The momentum parameter. A value of $0$ means no momentum.
$\beta_2$: The second moment parameter. A value of $0$ means no second moment adjustment.

The plots below show contour lines of the empirical loss function, i.e., two values that are on the same contour line have the same loss.

Question 1: Which parameter is varied here? Explain your reasoning.

Click for answer

The learning rate is varied. This can be seen as the gradient updates for the right trajectory are larger than for the left trajectory.

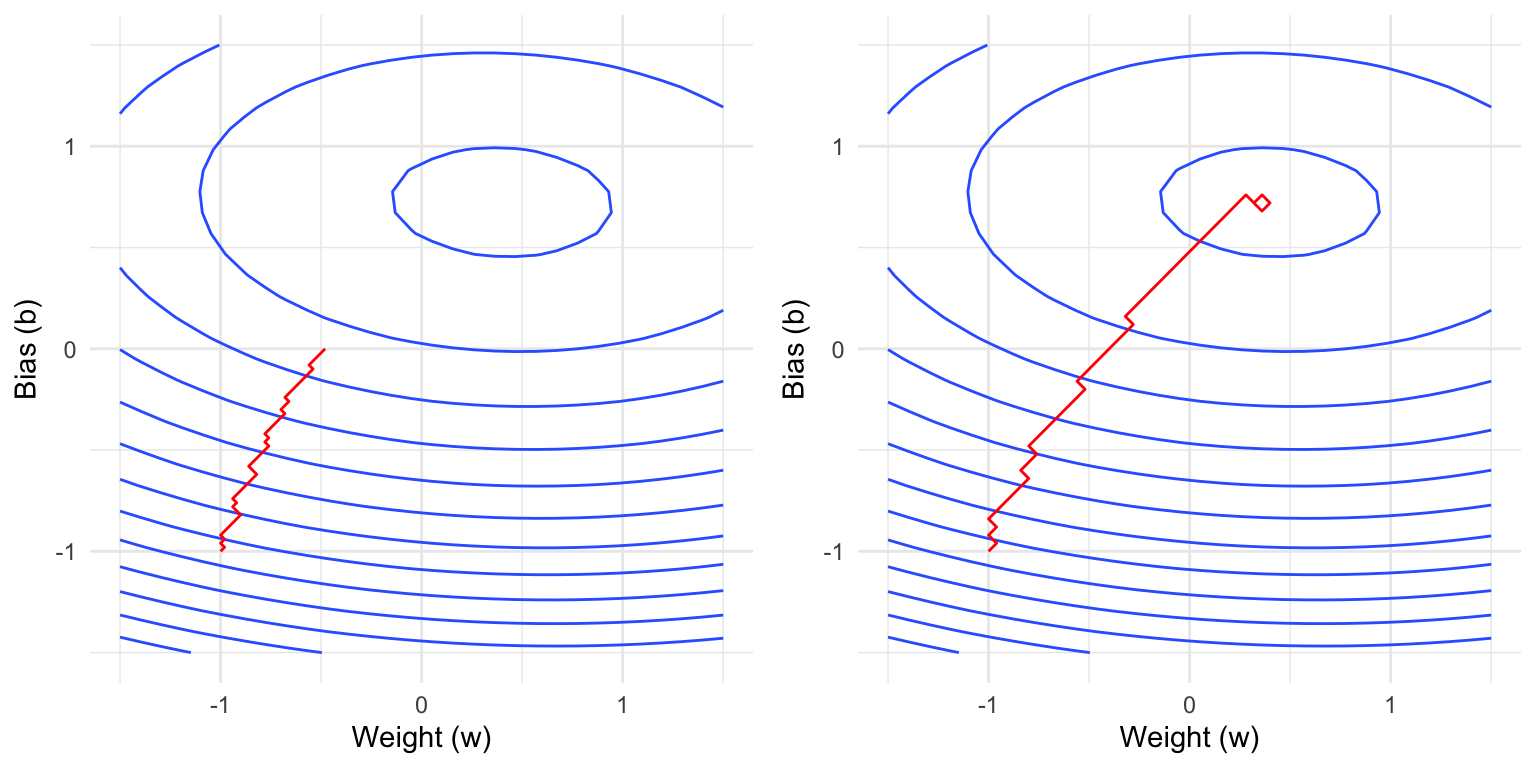
Question 2: Which parameter is varied below? Explain your reasoning.

Click for answer

The weight decay is varied. We can see this as the final parameter value for the right trajectory is closer to zero than for the left trajectory.

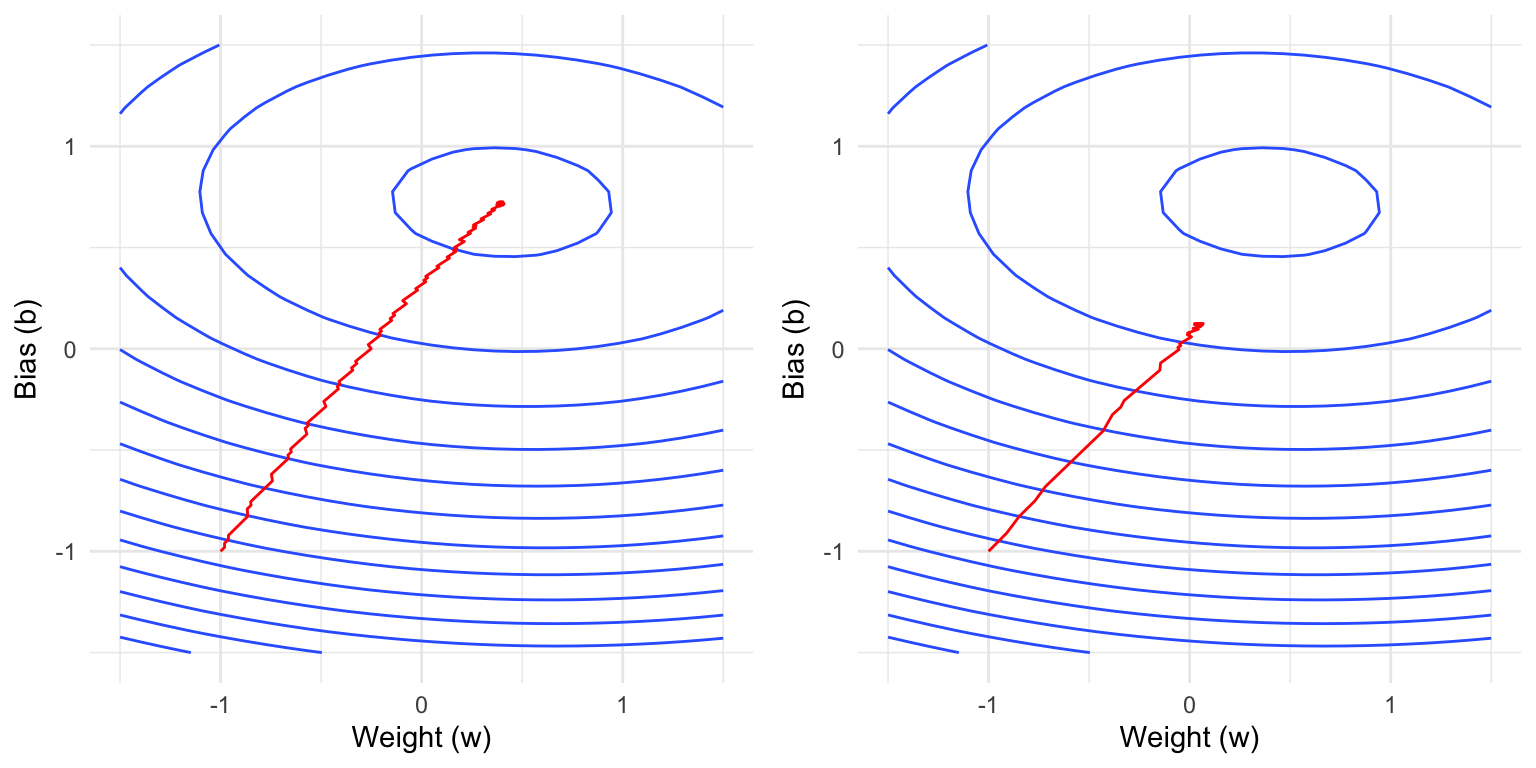
Question 3: Which parameter is varied below? Explain your reasoning.

Click for answer

The momentum parameter $\beta_1$ is varied. There is no momentum on the left side, so the gradient steps are more noisy. On the right side, the momentum is set to $0.9$, so over time, momentum in the ‘correct’ direction is accumulated.

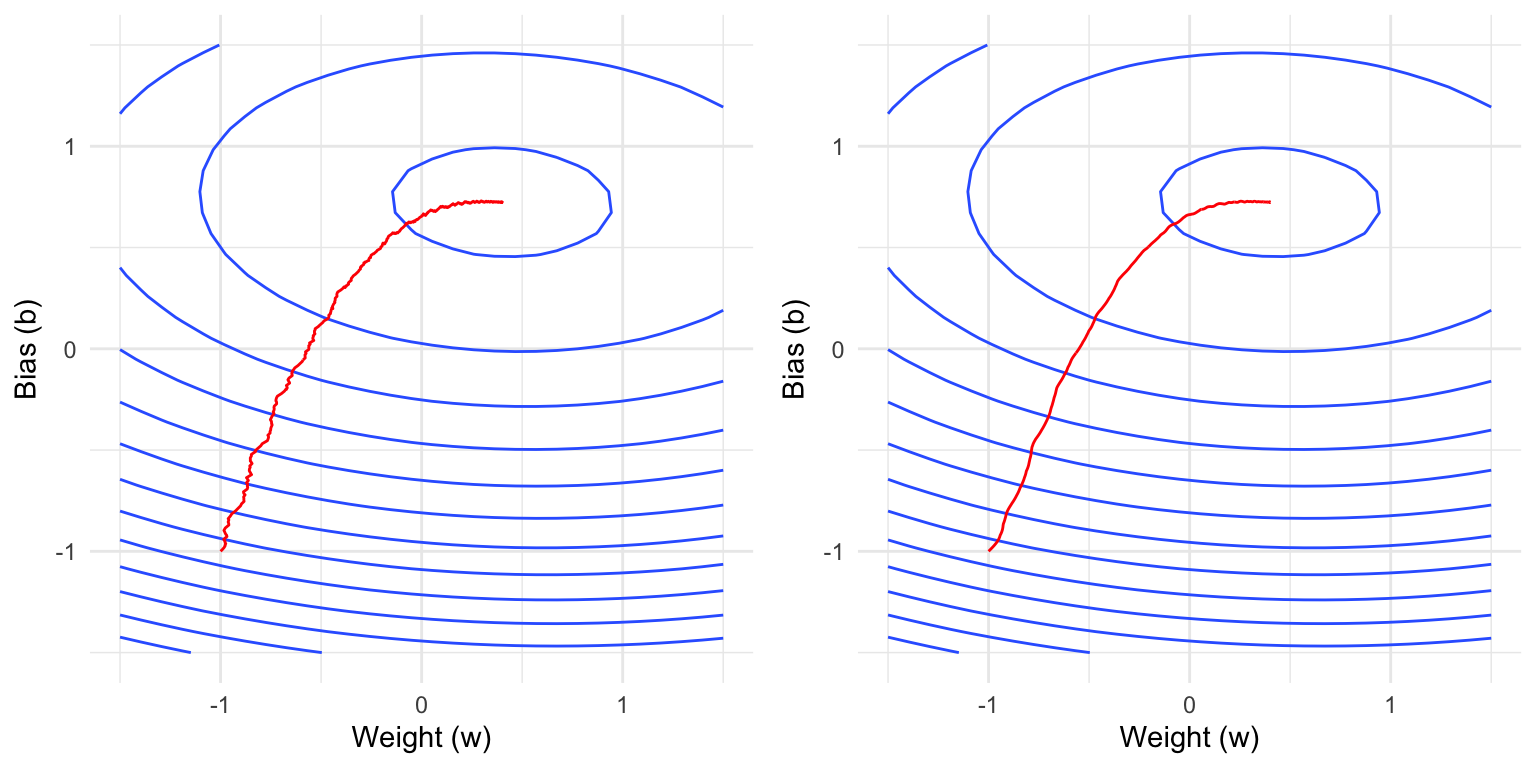
Question 4: Which parameter is varied below? Explain your reasoning.

Click for answer

The $\beta_2$ parameter is varied. There is no second moment adjustment on the left side, but there is on the right side. Because the gradients in the direction of the bias are larger than in the direction of the weight, the second moment adjustment helps to reduce the learning rate in the direction of the bias.

Learning Rate Schedules

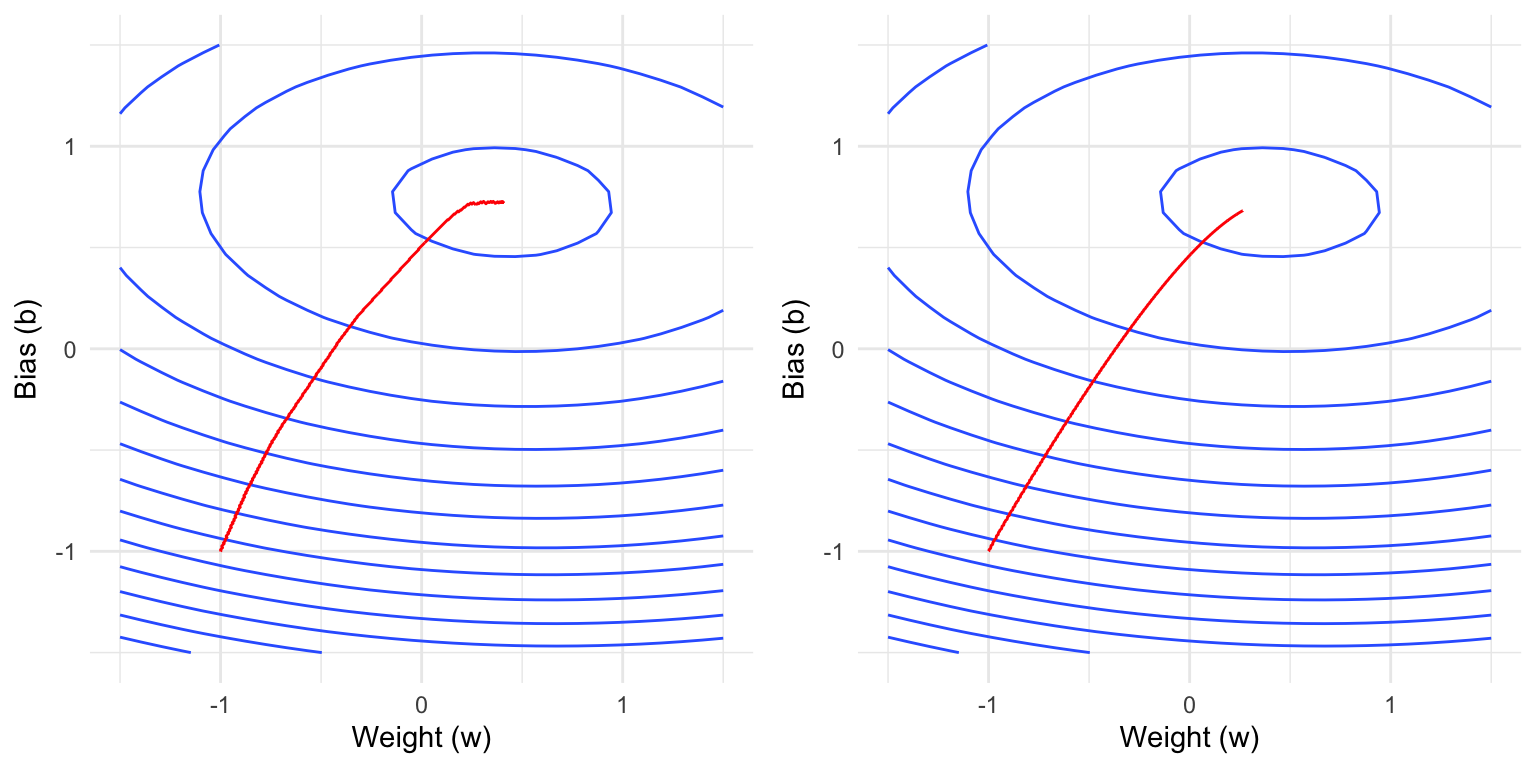
While we have already covered dynamic learning rates, it can still be beneficial to use a learning rate scheduler to further improve convergence. Like for adaptive learning rates, the learning rate is then not a constant scalar, but a function of the current epoch or iteration. Note that the learning rate schedulers discussed here can also be combined with adaptive learning rates such as in AdamW and are not mutually exclusive.

\[\theta_{t+1} = \theta_t - \eta_t \cdot \frac{\nabla_\theta L(\theta_t)}{\sqrt{v_t} + \epsilon}\]

Decaying learning rates:

This includes gradient decay, cosine annealing, and cyclical learning rates. The general idea is to start with a high learning rate and then gradually decrease it over time.

Warmup:

Warmup is a technique that gradually increases the learning rate from a small value to a larger value over a specified number of epochs. This ensures that in the beginning, where the weights are randomly initialized, the learning rate is not too high.

Cyclical Learning Rates:

Cyclical learning rates are a technique that involves periodically increasing and decreasing the learning rate. This can help the optimizer to traverse saddle points faster and find better solutions.

The different schedules are visualized below:

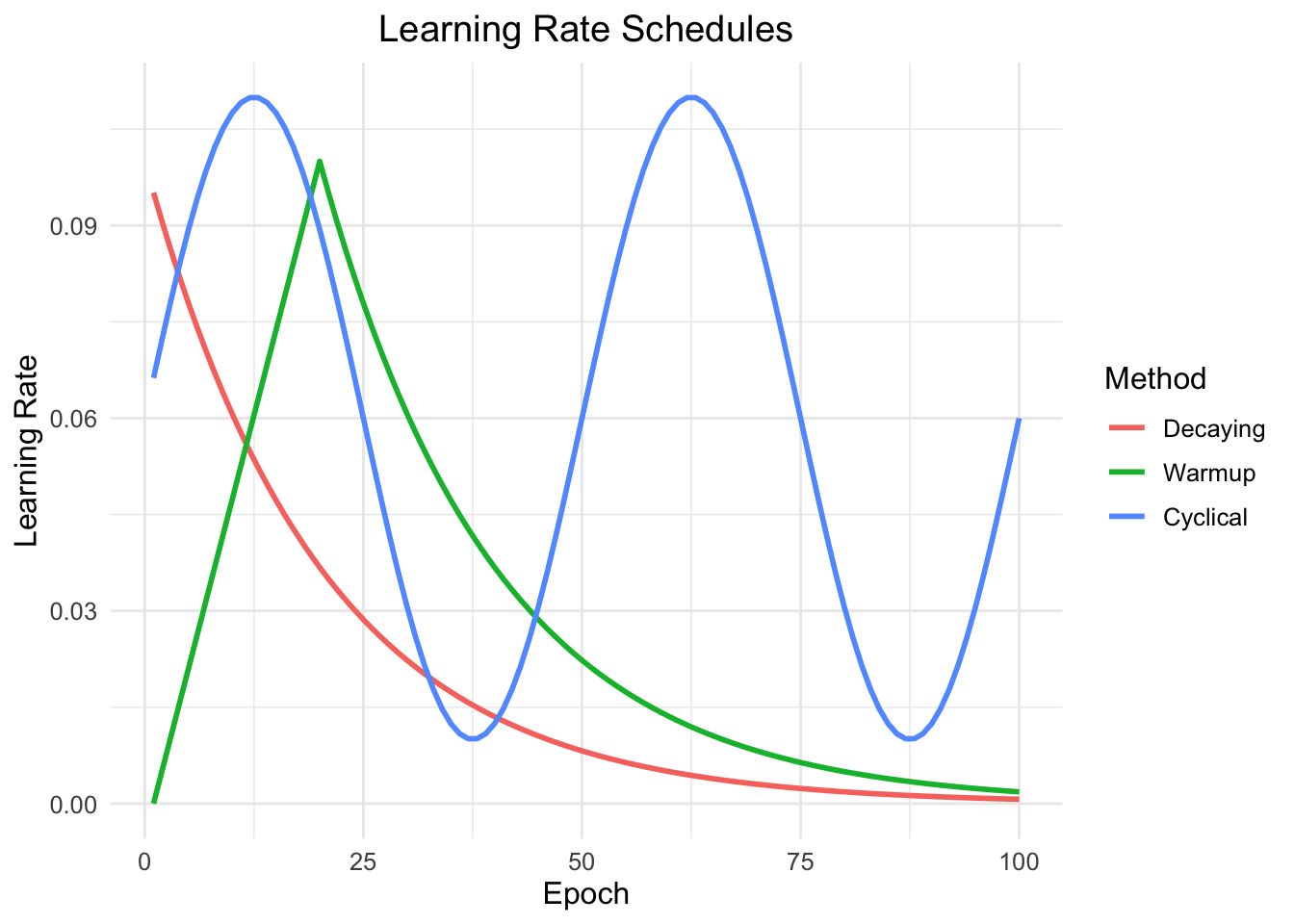
In torch, learning rate schedulers are prefixed by lr_, such as the simple lr_step, where the learning rate is multiplied by a factor of gamma every step_size epochs. In order to use them, we need to pass the optimizer to the scheduler and specify additional arguments.

scheduler = lr_step(opt, step_size = 2, gamma = 0.1)

The main API of a learning rate scheduler is the $step() method, which updates the learning rate. For some schedulers, this needs to be called after each optimization step, for others after each epoch. You can find this out by consulting the documentation of the specific scheduler.

opt$param_groups[[1L]]$lr

[1] 0.2

scheduler$step()
opt$param_groups[[1L]]$lr

[1] 0.2

scheduler$step()
opt$param_groups[[1L]]$lr

[1] 0.02

Saving an Optimizer

In order to resume training at a later stage, we can save the optimizer’s state using $state_dict().

state_dict = opt$state_dict()

This state dictionary contains:

The $param_groups which contains the parameters and their associated hyperparameters.
The $state which contains the optimizer’s internal state, such as the momentum and second moment estimates.

state_dict$param_groups[[1L]]

$params
[1] 1 2

$lr
[1] 0.02

$betas
[1] 0.900 0.999

$eps
[1] 1e-08

$weight_decay
[1] 0.01

$amsgrad
[1] FALSE

$initial_lr
[1] 0.2

Note

It is possible to set different parameters (such as learning rate) for different parameter groups.

o2 = optim_adamw(list(
  list(params = torch_tensor(1), lr = 1),
  list(params = torch_tensor(2), lr = 2)
))
o2$param_groups[[1L]]$lr

[1] 1

o2$param_groups[[2L]]$lr

[1] 2

The $state field contains the state for each parameter:

state_dict$state

$`1`
$`1`$step
torch_tensor
1
[ CPUFloatType{} ]

$`1`$exp_avg
torch_tensor
0.01 *
 5.9926
[ CPUFloatType{1,1} ]

$`1`$exp_avg_sq
torch_tensor
0.0001 *
 3.5912
[ CPUFloatType{1,1} ]


$`2`
$`2`$step
torch_tensor
1
[ CPUFloatType{} ]

$`2`$exp_avg
torch_tensor
0.01 *
 2.1779
[ CPUFloatType{1} ]

$`2`$exp_avg_sq
torch_tensor
1e-05 *
 4.7433
[ CPUFloatType{1} ]

Just like for the nn_module, we can save the optimizer state using torch_save().

pth = tempfile(fileext = ".pth")
torch_save(state_dict, pth)

Warning

Generally, we don’t want to save the whole optimizer, as this also contains the weight tensors of the model that one usually wants to save separately.

We can load the optimizer state again using torch_load().

state_dict2 = torch_load(pth)
opt2 <- optim_adamw(model$parameters, lr = 0.2)
opt2$load_state_dict(state_dict2)

Embedded Regularization Techniques

Besides the explicit regularization effects of weight decay and the implicit regularization effects of mini-batch gradient descent, there are also other regularization techniques that improve generalization of deep neural networks. Here, we focus on dropout and layer normalization, which are both embedded in neural network architectures.

Dropout

Dropout is a regularization technique used to prevent overfitting in neural networks. During each training iteration, dropout randomly “drops” a subset of neurons by setting their activations to zero with a specified probability. This forces the network to distribute the learned representations more evenly across neurons. Dropout is most commonly used in the context of fully connected layers.

Source

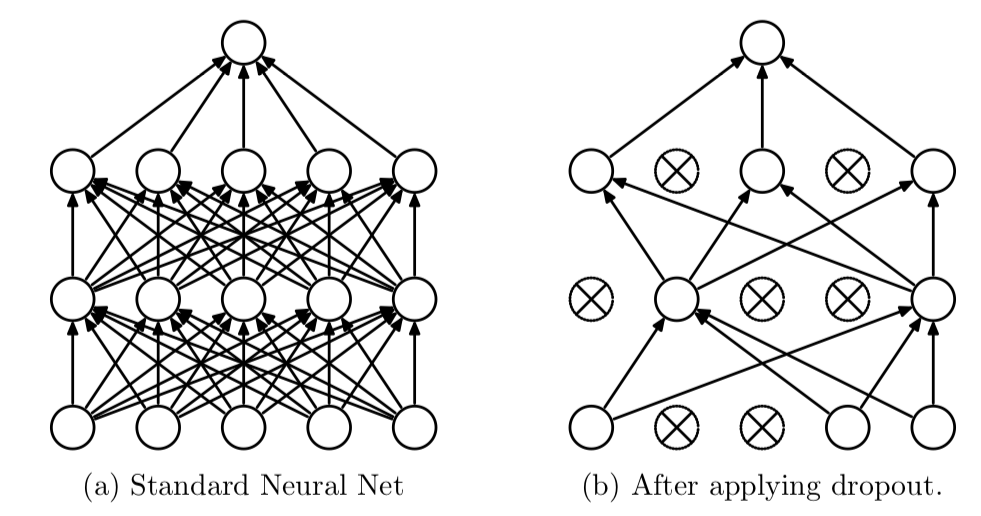
Note that neurons are only dropped when the module is in train mode, not in eval mode.

x = torch_randn(10, 5)
dropout = nn_dropout(p = 0.5)
dropout(x)

torch_tensor
-0.0000  3.7545  4.3769  0.0000  0.0000
 0.4759  0.7142  1.8560 -1.8215  0.0000
 0.0000  0.0000  0.8545 -1.1291 -0.0000
-0.0383  2.3208 -0.3911  2.5771  0.0000
 0.0000 -0.0000  0.0000  0.0000  0.0000
 0.6956  0.0000 -0.0000  2.9860  0.2500
-0.9978 -2.0387  0.0000  0.5153 -0.0000
-0.0000  0.0000 -0.9363 -0.0000 -0.7703
-0.9378 -0.2968  3.6971  1.6708 -0.0000
-0.0000  1.2085  0.0000  0.0000 -2.8396
[ CPUFloatType{10,5} ]

dropout$eval()
dropout(x)

torch_tensor
-0.4076  1.8772  2.1884  0.3678  0.0293
 0.2379  0.3571  0.9280 -0.9107  0.5313
 0.1559  0.1716  0.4273 -0.5645 -0.1329
-0.0192  1.1604 -0.1956  1.2885  0.3373
 0.3247 -1.6603  1.3701  1.0716  0.2485
 0.3478  2.6682 -0.4942  1.4930  0.1250
-0.4989 -1.0193  0.3470  0.2577 -0.4072
-0.4410  0.8347 -0.4681 -0.0240 -0.3851
-0.4689 -0.1484  1.8486  0.8354 -1.1521
-0.2673  0.6042  0.4407  0.5085 -1.4198
[ CPUFloatType{10,5} ]

Quiz: Dropout

Question 1: Worse Training Loss: You are training a neural network with and without dropout. The training loss is higher with dropout, is this a bug?

Click for answer

Not necessarily, as dropout is a regularization technique that prevents overfitting. Its goal is to reduce the generalization performance of the model and not to improve training performance.

Batch Normalization

Batch Normalization is an important technique in deep learning that contributed significantly to speeding up the training process, especially in convolutional neural networks that are covered in the next chapter. During training, batch normalization introduces noise into the network by normalizing each mini-batch independently. Besides faster congerence, batch normalization also acts as a regularizer, where the model learns to be less sensitive to the specific details of the training data, thus reducing overfitting.

The formula for batch normalization (during training) is given by:

\[ \hat{x} = \frac{x - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} \]

where:

$\hat{x}$ is the normalized output,
$x$ is the input,
$\mu_B$ is the mean of the batch,
$\sigma_B^2$ is the variance of the batch,
$\epsilon$ is a small constant added for numerical stability.

During inference, the module uses the running mean and variance of the training data to normalize the input.

In torch, different versions of batch normalization exist for different dimensions of the input tensor. Below, we illustrate the batch normalization module using a 1D input tensor (the batch dimension does not count here):

x = torch_randn(10, 5)
bn = nn_batch_norm1d(num_features = 5)
bn(x)

torch_tensor
 1.2203  1.1179  1.1652 -1.3292  0.5830
 0.6674 -1.1404 -0.1058  0.1933 -0.4474
 0.2395  0.6881  1.0513 -1.2640 -0.2211
-1.9849  0.2075 -0.3904  0.5686  1.6812
-0.5494 -0.9593 -1.6051 -1.3635  0.3326
 0.4905  1.1264  0.4455  0.8893 -0.3957
-0.9948 -0.0520 -0.2290  0.1912 -1.1758
-0.5657 -1.3184 -1.8173  1.1717 -1.8676
-0.0116  1.3793  0.4786  1.4124  1.1464
 1.4886 -1.0491  1.0071 -0.4698  0.3644
[ CPUFloatType{10,5} ][ grad_fn = <NativeBatchNormBackward0> ]

Quiz: Batch Normalization

Question 1: Earlier we have learned that nn_modules have buffers and parameters, where only the latter are learned with gradient descent. Do you think the mean and variance are parameters or buffers?

Click for answer

They are both buffers as they only store the variance and running mean of all training samples seen, i.e., they are not updated using gradient information.

Question 2: Training vs. Evaluation Mode: While many nn_modules behave the same way irrespective of their mode, batch normalization is an example of a module that behaves differently during training and evaluation. During training, the module uses the mean and variance of the current batch, while during evaluation, it uses the running mean and variance of all training samples seen.

bn(x[1:10, ])

torch_tensor
 1.2203  1.1179  1.1652 -1.3292  0.5830
 0.6674 -1.1404 -0.1058  0.1933 -0.4474
 0.2395  0.6881  1.0513 -1.2640 -0.2211
-1.9849  0.2075 -0.3904  0.5686  1.6812
-0.5494 -0.9593 -1.6051 -1.3635  0.3326
 0.4905  1.1264  0.4455  0.8893 -0.3957
-0.9948 -0.0520 -0.2290  0.1912 -1.1758
-0.5657 -1.3184 -1.8173  1.1717 -1.8676
-0.0116  1.3793  0.4786  1.4124  1.1464
 1.4886 -1.0491  1.0071 -0.4698  0.3644
[ CPUFloatType{10,5} ][ grad_fn = <NativeBatchNormBackward0> ]

Which of the following statements is true and why?

bn$eval()
equal1 = torch_equal(
  torch_cat(list(bn(x[1:2, ]), bn(x[3:4, ]))),
  bn(x[1:4, ])
)
bn$train()
equal2 = torch_equal(
  torch_cat(list(bn(x[1:2, ]), bn(x[3:4, ]))),
  bn(x[1:4, ])
)

Click for answer

c(equal1, equal2)

[1]  TRUE FALSE

The first statement is true because, in evaluation mode, the module uses the running mean and variance of all training samples seen. The second statement is false because the first tensor uses different means and variances for rows 1-2 and 3-4, while the second tensor uses the same mean and variance for all rows.

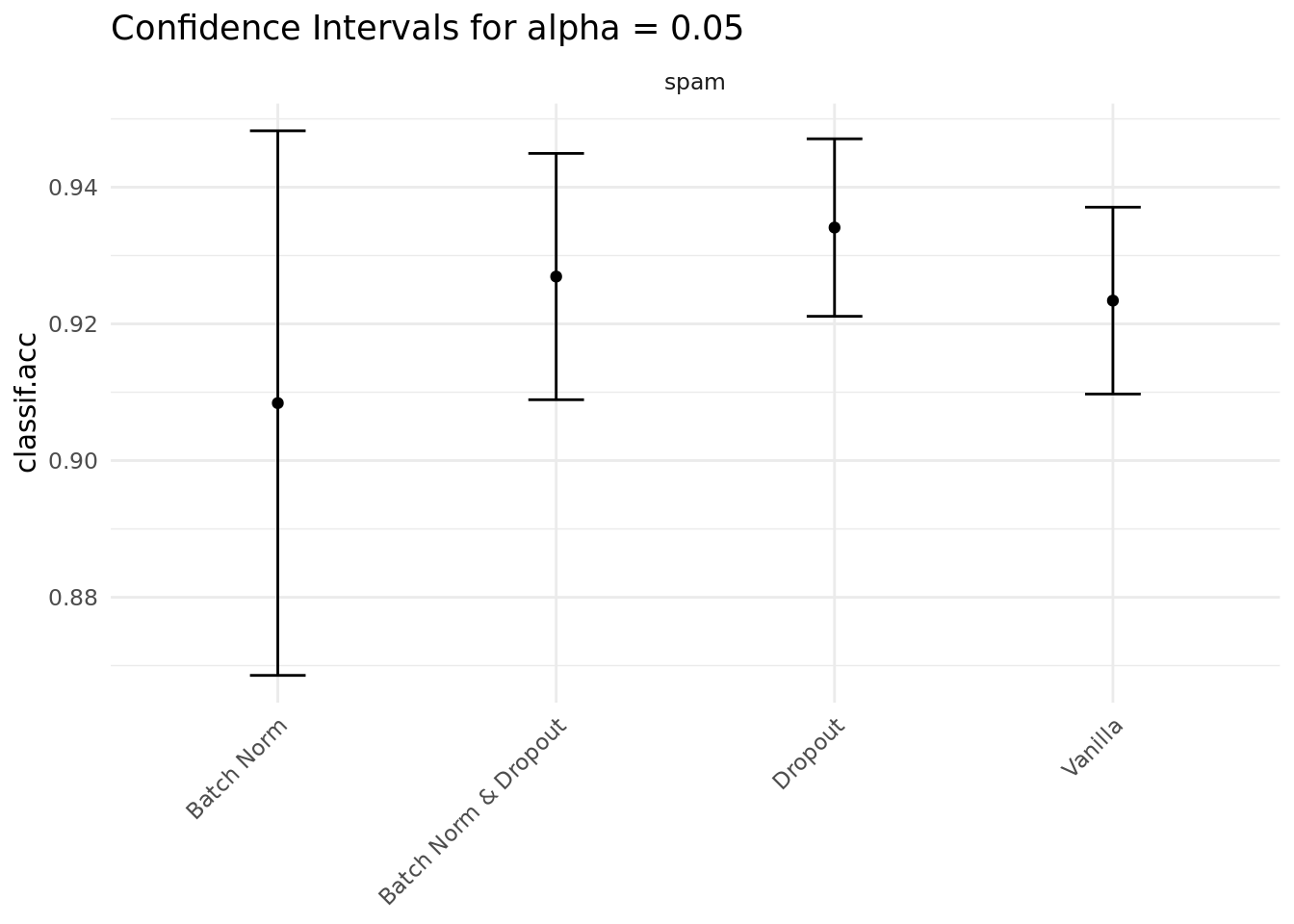
To demonstrate these dropout, we apply them to a simple spam classification task. The data has one binary target variable type (spam or no spam) and 57 numerical features.

c(nrow(spam), ncol(spam))

[1] 4601   58

table(spam$type)


   spam nonspam 
   1813    2788

Below, we create a simple neural network with two hidden layers of dimension 100, ReLU activation and optionally dropout and batch normalization.

nn_reg <- nn_module("nn_reg",
  initialize = function(dropout, batch_norm) {
    self$net <- nn_sequential(
      nn_linear(in_features = 57, out_features = 100),
      if (batch_norm) nn_batch_norm1d(num_features = 100) else nn_identity(),
      if (dropout) nn_dropout(p = 0.5) else nn_identity(),
      nn_relu(),
      nn_linear(in_features = 100, out_features = 100),
      if (batch_norm) nn_batch_norm1d(num_features = 100) else nn_identity(),
      if (dropout) nn_dropout(p = 0.5) else nn_identity(),
      nn_relu(),
      nn_linear(in_features = 100, out_features = 2)
    )
  },
  forward = function(x) {
    self$net(x)
  }
)
nn_drop <- nn_reg(dropout = TRUE, batch_norm = FALSE)
nn_batch <- nn_reg(dropout = FALSE, batch_norm = TRUE)
nn_both <- nn_reg(dropout = TRUE, batch_norm = TRUE)
nn_vanilla <- nn_reg(dropout = FALSE, batch_norm = FALSE)

We evaluate the performance of the four neural networks created above using subsampling with 10 repetitions and an 80/20 train/test split. We don’t show the specific training code here, but only the resulting confidence intervals for the accuracy. While the intervals are too wide to be able to draw any final conclusions, both regularizaion techniques tend to lead to better results. Also, both normalization techniques improve stability, so that the confidence intervals are narrower.

References

Loshchilov, I. 2017. “Decoupled Weight Decay Regularization.” arXiv Preprint arXiv:1711.05101.